Understanding 4-20mA Current Loop Communications

Imagine this: You’ve got your flow meter with 4-20mA output setup. Confidently, you flip the switch, turning it on and then it happens–the readings are off. You’re not getting the output you need. Frustrated, you tinker with it, and still nothing. Now, you’re out of your depth. You need to get this thing working so you can get your application up and running.

What are you going to do? Who are you going to call to get help? Why is this even happening?

Many times, I get asked by customers “how do I get accurate 4-20mA output readings?” for 4-20mA output devices. What I have found most helpful for customers is an understanding of the basics of 4-20mA current loops and how it integrates into their process.

Today, we’re going to go over the 4-20mA communications protocol, step-by-step. This will dispel the complications and confusion around the protocol and help you get set up and running.

What Are the Different Ways to Determine Flow Rate?

There are times when we need to determine what the flow rate is (or temperature, or pressure) without looking at the meter’s display. There are a few ways to do this:

1. Utilizing the RS-232 serial commands

2. Utilizing Modbus, HART, or other supported digital communications protocols

3. Utilizing the 4-20mA support within the meter

What is a 4-20mA [Direct Current] Loop?

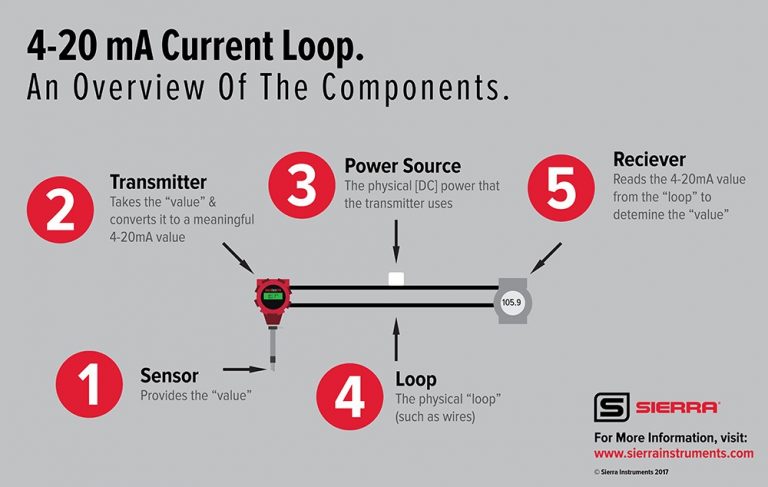
A 4-20mA current loop is a means to pass a “value” like flow using an established electrical current (the loop) as the carrier of this information.

There are 5 discrete parts to the “loop” (see image above):

1. Sensor: Provides the “value”

2. Transmitter: Takes the “value” and converts it to a meaningful 4-20mA value

3. Power Source: The physical [DC] power that the transmitter uses

4. Loop: The physical “loop” (such as wires)

5. Receiver: Reads the 4-20mA value from the “loop” to determine the “value”

Generally, the 4mA represents the minimum/low value (like 0 for flow); and the 20mA represents the maximum/high value, or full scale, of the value you are sending. In our example, this value is for “flow.”

How Do You Map/Configure the 4-20mA Current Loop to the Flow Rate?

Most people I talk to overthink the math for 4-20mA in their application. It would be like using calculus to solve a simple math problem. It’s not that complicated, once you understand the values used in the equation.

As mentioned above, the 4mA represents “zero” [flow], and the 20mA represents the full scale.

So, if our flow setup is 0 to 1000 SLPH, the 4mA means “0” flow, and the 20mA means “1000”.

The Variables In the 4-20mA Equation

We can represent the flow range using the following notations:

Now if we are flowing 500, we use the following notation:

Because we know that the value we want to pass on the 4-20mA loop is really a ratio between mALow to mAHigh, we apply the following formula to determine the correct milliamps (mA) we need to be at:

So, in our current 4-20mA example, flowing 500 is represented as 12mA on the 4-20mA loop. If we were flowing zero (currentValue=0), we would calculate it as:>

If we were flowing Full Scale (currentValue=1000), then we would calculate:

What if my scale is different? How would we scale to a 0-20mA loop instead of the 4-20mA loop?

If we wanted to scale from 0 to 20 instead of 4 to 20, all we do is change the value of mALow to “0” instead of “4”. The same formula works. Don’t forget that fact. The only things that change are the values of the variables.

So, if we are flowing 500 (currentValue=500) on a 0/20mA loop, we set the loop to:

How would we scale something like temperature that DOES NOT have a low value of “0”?

When we deal with temperature, we generally do not start at 0f, but 32f. All we need to do is adjust the “mAValueLow” to the new low value. Let’s assume our working temperature is 32°f ~ 132°f:

Now we apply the same formula. So if our temperature is 82°f (currentValue=82), use the formula:

Bringing It All Together

Alright, time to do some math! To summarize what we have talked about, use the following formula to determine the 4-20mA values:

Fine Tuning the 4-20mA Signal

At this point, we are able to determine the correct value for the 4-20mA signal utilizing the formula above. But what happens if we are flowing zero, and the output should be 4mA, but, because of the physical layout, the receiver “reads” 3.90mA? In other words, the 4mA default “low” 4mA value needs to be “tuned” higher to 4.0mA. We would need to change the default 4mA DAC (Digital to Analog Converter) value.

Understanding DAC’s and Their Relationship to 4/20mA Current Loop

When we want the 4-20mA transmitter to inject a 4-20mA signal, it needs to “know” exactly how much to inject. You can think of the DAC’s as a [digital] valve that can go from totally closed, to totally open; or anything in-between.

The range from closed to fully open is defined in 4096 “steps”; meaning, that each step “opens” the “valve” by 1/4096 in size.

By setting the 4mA DAC to “1” means that we “open” the valve 1/4096 in size to represent 4mA. Setting the 4mA DAC to 2048 (2048/4096 = ½) will open the “valve” exactly halfway open. Setting the DAC to 4096 will open the “valve” fully open.

By adjusting the 4mA or 20mA DAC’s, we can fine-tune the electrical characteristics of the 4-20mA loop. Once we have fine-tuned the lower 4mA and the higher 20mA DAC’s, the system will correctly calculate the points in-between.

In Conclusion

By setting the correct values in the 4-20mA screens, along with the any DAC adjustments, you can make the meter provide 4-20mA “answers” correctly. This gives you accurate output readings so you can run your application and make adjustments to get optimal conditions.

If you have any questions or comments, please contact Kam Bansal, Director of Engineering.